说一下我的理解,欢迎指正。
泛函(functional)通常是指定义域为函数集,而值域为实数或者复数的映射,换句话说,它是从函数组成的一个向量空间到标量域的映射,它的输入为函数,而输出为标量。
这里把泛函和函数、算子的概念区别理解一下。
简单来说,算子是一个函数到另一个函数的映射,它是从向量空间到向量空间的映射,泛函是从向量空间到数域的映射,函数是从数域到数域的映射
举一个泛函的例子:两点之间直线距离最短
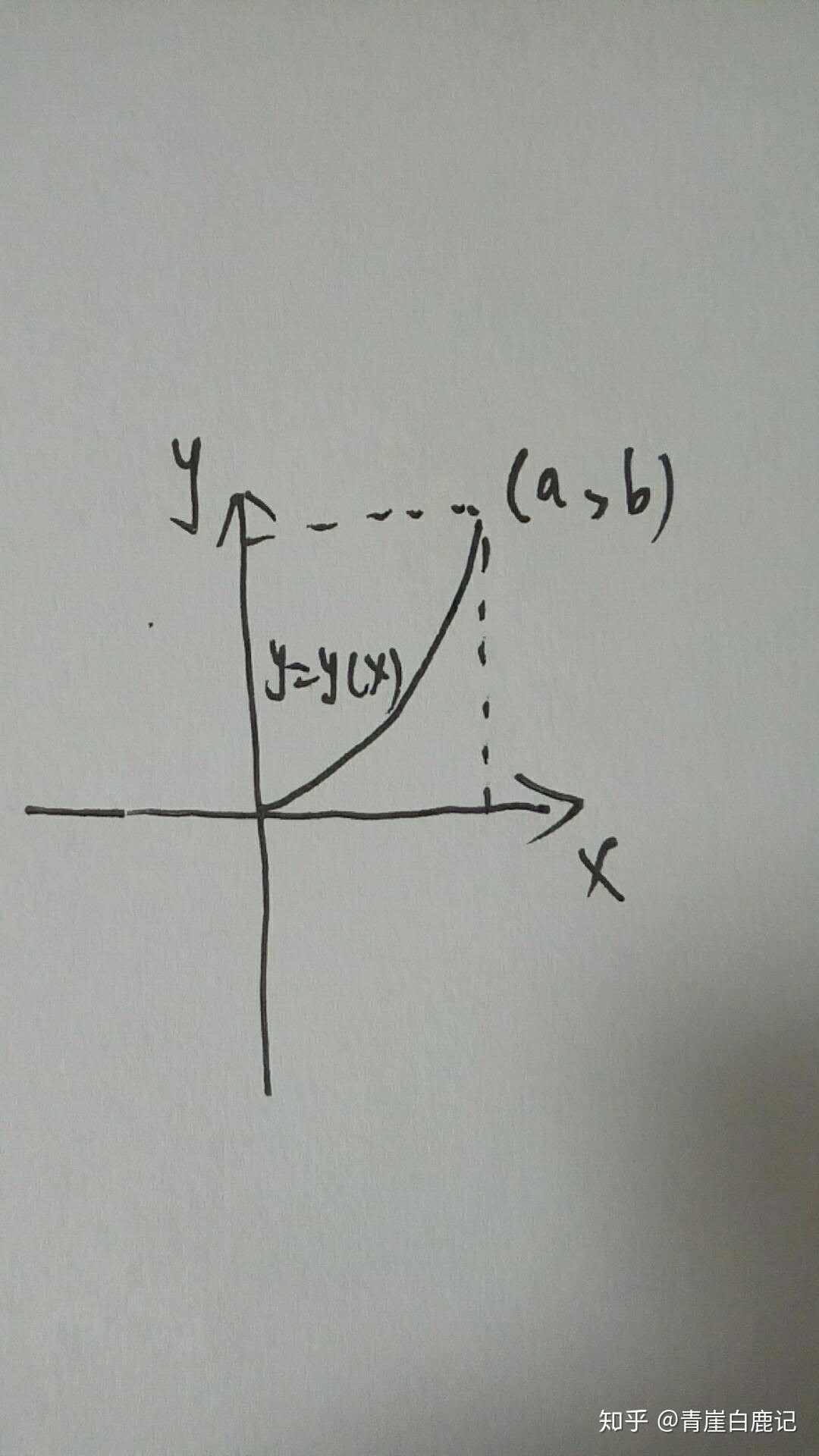
如图所示二维平面空间,从坐标原点(0,0)到点(a,b)的连接曲线是 y=y(x)
曲线的弧长微元是
曲线的总弧长是
其中s是标量,上式右边是 的广义函数,被称为泛函,可记为
问题变成了:找出曲线y(x),使得泛函 最小。
这个问题可以用变分法求解。
把函数变成数的变换
有回答说:“泛函(functional)通常是指定义域为函数集,而值域为实数或者复数的映射,换句话说,它是从函数组成的一个向量空间到标量域的映射,它的输入为函数,而输出为标量。”这句话是对的吗?
这个回答是不精确的。一个从无限维流形到数域的映射也是泛函。也就是说,函数空间可并不一定是一个向量空间!
———————————————————————————
函数:将 中的元素(向量)映射到实数轴
(一维线性空间)或者复平面。微积分学(包括复变函数论、实变函数论)对“函数”进行了透彻的研究。
对于函数集合,比如 中的开集
上的全体连续函数,这个集合中每一个元素都是函数。如果在这个函数集合上引入拓扑结构,那么“集合”就成为“空间”,称为“函数空间”。函数空间往往是无限维的线性拓扑空间。所谓“泛函分析”一般分为两个层次:
线性泛函分析:研究的是无限维线性空间和线性映射。如果一个线性映射,将无限维空间中的元素映射到实数轴 (复平面也可),则称为“线性泛函”。线性泛函分析这门学科的目的就是:
(1).试图将线性代数的相关理论类比推广到无限维空间中去。在这方面最重要的结果就是Hahn-Banach定理和Riesz表示定理。
(2).由于无限维空间有界集不再是列紧集,“紧性”在分析学中是极其重要的。因此有必要研究无限维线性空间的拓扑,为此需要引入弱收敛、弱 * 收敛等概念。
(3).分析学研究空间与映射。因此除了在无限维空间引入不同的拓扑之外,线性泛函分析需要研究线性映射的性质。当然这里的线性映射不再局限于线性代数的有限维空间上的映射。这方面最重要的结果集中在Baire纲定理的一系列结果。
非线性泛函分析:研究无限维“非线性”空间——也就是无限维流形,以及非线性映射。
如果一个非线性映射,将无限维空间中的元素映射到实数轴 (复平面也可),则称为“非线性泛函”。
泛函 直接翻译就是功能函数。
一般的函数是这样的
y=x+1
泛函是这样的
y=1?1
?为+的时候,y=2
?为 -的时候y=0
说白了,定义域为{+, -},值域为{0, 2}
输入一个算子输出一个结果
大概是这个意思。
当然,正儿八经的泛函复杂的多,因为我们平常用的加减法算式是基于算子不能改变而设计的,没办法表达泛函,所以泛函加了更多复杂的符号记号,但是意思大差不差是这个意思
泛函是高阶逻辑,可以对计算规则本身进行计算,所以很重要。编程里用的多
别的回答都是什么牛鬼蛇神。
函数是可以构成一个集合的,简单的讲从一个集合到数集的映射称为泛函。如此函数的函数可以作为泛函的特例。

参考上图,以及个人知识储备,函数是泛函,泛函是映射,即它们都是映射的特例,而实变函数、复变函数是函数的特例,线性泛函是泛函的特例(线性泛函说的是线性空间出发到复值域的线性映射。)
类似实变函数和复变函数,泛函分析主要是对泛函进行研究,同样因为这样的函数有很好的结构和性质。正如前面一篇回答提到的迭代法,在泛函中也有很好的应用。下面举例说明
考虑到基础不太好的读者,文末会补充一下基础概念,再回到这里读起就会轻松许多。


等价积分方程是很显然的,因为X'(t)是等于右边在t定义内连续,并且利用微积分基本定理可以得到。充分性的话,由f(t,x(t))连续故可积故X(t)可导,同时带入t知X(t)=X(t0)。
考虑到压缩映像原理。构造一个泛函-T,要保证T是压缩的同时希望T的不动点就是方程的解(相反若为方程解容易得到这个解是不动点)。这样就几乎证明了定理。(因为最初的初值问题的解要在T的不动点中寻找,而T的不动点又是原初值问题的解,如果T的不动点唯一且在定义区间连续就证明了定理)
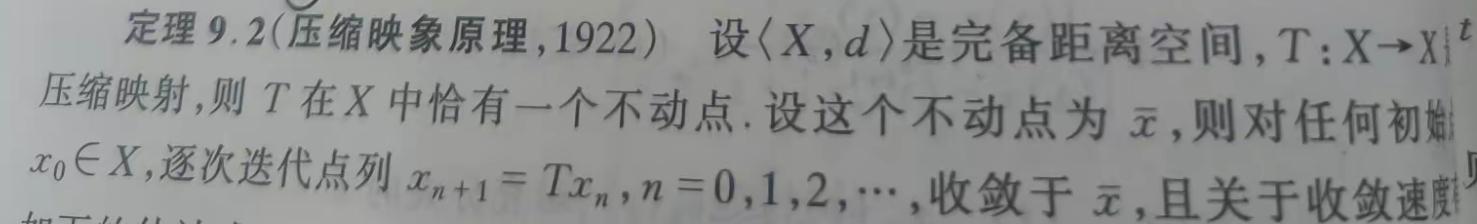

然后我还希望这个解是连续的,准确的说在定理结论区间连续,记为k。自然的我定义这个泛函的起点为k内的连续函数全体(这是个距离空间是很容易的,定义距离d=max|x(t)-y(t)|,t取遍k),而且容易证明这是个完备的距离空间(文末给了一个类似证明)。
T在k内是压缩的按定义便可给出证明,希望读者自行验证。
然后我们来证明压缩映像原理,最后便完成了这个定理证明。
构造这样一个迭代点列Xn+1=TXn, 如果能证明T是连续的,那由函数连续的几条等价定义便容易得到这个不定点。

但是你会发现为什么这个序列是收敛的呢?然后回头看条件之一距离空间是完备的。进而只需证明它是Cauchy列,

稍微解释一下,证明cauchy例就是说对任给一个大于0的数e,总是对所有充分大的n满足d(Xn+k,Xn)比e要小对正整数k总成立,最后一步是为了让k消失,从而确定这个使k一致的n要怎么充分大,才能使所有n都满足这个不等式(这个本来是很自然的)
这也解释了为什么要做这样的迭代。(刚好这是一个cauchy列,若如不然这个迭代方程应该具有什么样的形式)
最后细心的读者会发现T连续只是假设,这个证明是很容易的,利用定义即可(和前面证明压缩映射类似),另外这个不动点是唯一的是也是很容易证明的(反证推出矛盾即可)。
最后梳理一下上述证明。只需要有个不动点以及转换等价积分方程的意识,进而做适当的构造、推理,定理也就证明了
读者可以比较另一篇回答的迭代法,这样对泛函的理解也就有了一定层次。同时也加深了迭代法的理解。迭代相关的作品目前共有三篇感兴趣的读者可以看看。
注:线性空间说的是某个数域上的线性空间在其上的运算满足八条性质,距离空间说的是定义了距离d的空间,其中d满足三条性质(主要是传递性d(x,z)≤d(x,y)+d(y,z))。完备空间说的是距离空间中的任何cauchy列都收敛。下面给出一个证明

作为结语,第一次发布有许多谬误及不足,修改过后若有不足希望读者与我交流,这样我能够为大家提供更好,更准确的作品









